Los últimos días del mes tienen menos opciones. Hay otra forma de verlo que pone de manifiesto la pequeña desviación. Pongamos un día del mes que no sea cercano al principio ni al final del mismo. La pinta que tendría sería tal que así:
_ _ _ B _ _ _
Ahora vamos a marcar con una X los días en los que no puede hacerse la barbacoa:
1) _ X _ B _ _ _
2) _ _ X B _ _ _
3) _ _ _ B X _ _
4) _ _ _ B _ X _
Como podemos observar, para cada día normal (i.e. no en los extremos del mes), hay 4 días prohíbidos: dos anteriores al día elegido, y dos posteriores. Sin embargo, hay que darse cuenta de que los días anteriores ya los hemos contado con anterioridad. Siguiendo con nuestro ejemplo, las dos X previas a B, han sido contadas cuando se revisaron el segundo y tercer día del mes (nótese que el orden no importa, por lo que XB es igual que BX):
1) _ _ B X _ _ _ (ésta es igual que la opción 2 arriba)
2) _ B _ X _ _ _ (ésta es igual que la opción 1 arriba)
Por lo tanto, para cada día podemos considerar que existen dos combinaciones prohíbidas: las dos construídas usando días posteriores. Sin embargo, los días del final del mes no tienen dos días posteriores. Examinamos el penúltimo y el último día:
Penúltimo) _ _ _ _ _ B _ (días prohíbidos aún no contados: 1)
.....Último) _ _ _ _ _ _ B (días prohíbidos aún no contados: 0)
Con estos datos, el número de combinaciones prohíbidas es tal que
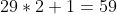
. O reescrito por simplicidad:
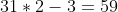
Formas de poner dos barbacoas en Julio (el orden no importa):
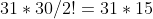
Restamos:
 = 31*15 - 31*2 + 3 = 31(15-2) + 3 = 31*13 + 3 = 403 + 3 = 406)
Soooo, unless I'm wrong again, the answer is
406.





