Pero creo que la respuesta está bien.respuesta: show
La mediana de un conjunto de 6 números es la media de los dos elementos centrales. Necesitamos averiguar en qué posiciones caerían las variables X e Y, y sus signos, para determinar si la mediana es positiva. Recolocamos los números en orden por el momento: -8 3 4 6.
(1) Nos dice que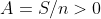
, o lo que es lo mismo que la suma de los elementos es positiva: 
. La suma de los valores conocidos es 
, por lo que la diferencia de X e Y no puede superar 5. Además, la única forma de que la mediana fuera negativa, sería que ambos valores fueran negativos.
Si cogemos los valores negativos más pequeños posibles para X e Y (i.e. X=-1, Y=-1), nos queda: -8 -1 -1 3 4 6, con media positiva y mediana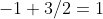
positiva.
Si elevamos uno de los valores para que al sumar con 3 el resultado sea negativo o cero, nos queda: -8 -3 -3 3 4 6, con media negativa y mediana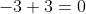
no positiva. Esto viola el dato de que la media es positiva, por lo tanto no son valores válidos de X e Y. Podemos deducir que la mediana es siempre positiva. Suficiente.
(2) Nos dice que X e Y tienen signos opuestos y ninguno es cero. Eso quiere decir que la mediana se va a calcular con 3 y un valor positivo, y por lo tanto será positiva. Suficiente.
La respuesta es (D).
(1) Nos dice que
Si cogemos los valores negativos más pequeños posibles para X e Y (i.e. X=-1, Y=-1), nos queda: -8 -1 -1 3 4 6, con media positiva y mediana
Si elevamos uno de los valores para que al sumar con 3 el resultado sea negativo o cero, nos queda: -8 -3 -3 3 4 6, con media negativa y mediana
(2) Nos dice que X e Y tienen signos opuestos y ninguno es cero. Eso quiere decir que la mediana se va a calcular con 3 y un valor positivo, y por lo tanto será positiva. Suficiente.
La respuesta es (D).
